看了很多博客文章书,发现学懂是一回事,能讲明白是另一回事。知乎推荐了一个课程,Coursera上的机器学习课程(免费),授课是斯坦福大学的老师,看了第一周的内容,感觉讲的很好,从基础入手,很详细,整理大致内容如下:
1.什么是机器学习
Arthur Samuel定义:the field of study that gives computers the ability to learn without being explicitly programmed. 这个定义比较老旧,大意是一种学科专门研究让电脑不经过特定编程而是通过自我学习完成某项任务。
Tom Mitchell提出的现代定义:A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
很押韵,但是我蹩脚的Chinglish是读不出来了,,,大意为:机器学习算法可以从过去已知的数据中学习数据隐藏的规律,利用这些学习来的规律,在给定一定输入的情况下,对未来进行预测
2.分类
Supervised learning and Unsupervised learning 监督学习或无监督学习
2.1.监督学习
在监督式学习中,我们给了一个数据集,并且已经知道我们的正确输出应该是什么样子,并且有输入和输出之间有关系的想法。监督学习问题分为“回归”和“分类”问题。
2.1.1.回归问题,这里我们试图预测连续输出中的结果,这意味着我们试图将输入变量映射到某个连续函数。例如:给定一个人的照片,我们必须根据给定的图片来预测他们的年龄。
2.1.2.分类问题,这里我们试图预测离散输出的结果。换句话说,我们试图将输入变量映射到离散类别。例如:给患有肿瘤的患者的肿瘤数据,我们必须预测肿瘤是恶性的还是良性的。
2.2.无监督学习
无监督的学习使我们能够很少或根本不知道我们的结果应该是什么样子。 我们可以从数据中推导出结构,我们不一定知道变量的影响。我们可以通过基于数据中变量之间的关系对数据进行聚类来推导出这种结构。在无监督学习的基础上,没有基于预测结果的反馈。
聚类问题就是典型的无监督学习。看到这里觉得我们研究的复杂网络社团划分其实也可以说是无监督学习问题,应该吧~
3.监督学习的模型
监督学习的模型是:从给定的训练数据集中,获得一个好的预测模型,再由预测模型获得待测试数据的结果。

当我们试图预测的目标变量是连续的时候,我们把学习问题称为回归问题。 当y只能接受少量的离散值时,我们称之为分类问题。
4.成本函数
我们可以使用成本函数来衡量我们的假设函数的准确性。 这个假设的所有结果的平均差异与来自x的输入和实际输出y的输入。

这个函数被称为“平方误差函数”或“均方误差”。 由于平方函数的导数项将抵消1/2,因此平均值减半(除以2),以方便计算梯度下降。
当然这么说实在是很枯燥,我们希望能更直观的去理解它。现在假设我们的训练数据集散布在x-y平面上,我们试图做一条直线(由hθ(x)定义)通过这些散布的数据点。
我们的目标是获得最佳线路。 理想中最好的线是——从实际点到目标函数的平均垂直距离最小。 理想情况下,这条线应该通过我们的训练数据集的所有点。 在这种情况下,J(θ0,θ1)的值将为0。以下示例显示了具有0的成本函数的理想情况。
该成本函数hθ(x)=θ1*x(θ0 = 0,即只考虑一个变量函数)

其中左图为成本函数图像,右图为均方误差图像,可以看出当θ1取1时,该误差为0,接下来试用不同的θ1计算均方误差,当θ1= 0.5时,我们看到我们的拟合直线到数据点(实际点到目标函数)的垂直距离增加。同时标记均方误差函数曲线。

这样,我们在使用不同的θ1时,我们可以得到一个均方误差图像如图所示。

因此,我们的目标就是我们应该尽量减少均方误差值。 在这种情况下,θ1= 1是我们的全局最小值。
轮廓图是包含许多轮廓线的图形。即两个变量函数的轮廓线在同一行的所有点上具有恒定值。 这个图的一个例子就是下面的一个例子。
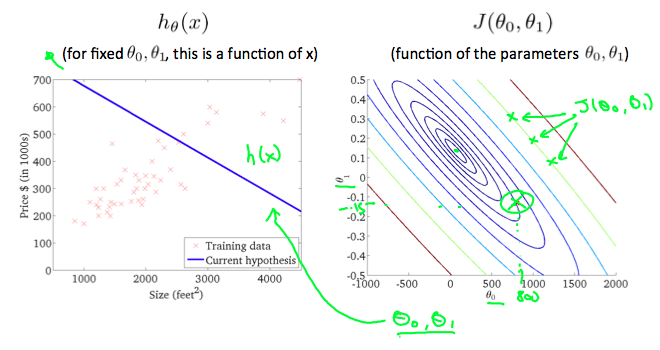
在任何一个圈,我们都会期望获得相同的成本函数值。例如,上面绿线上的三个绿点对于J(θ0,θ1)具有相同的值。带圆圈的x显示当θ0= 800和θ1= -0.15时左侧图形的成本函数的值。 再取一个h(x)并画出它的等高线图,可以得到上图;当θ0= 360且θ1= 0时,等值线图中J(θ0,θ1)的值更靠近中心,从而降低了成本函数误差。 现在给我们的假设函数一个略正的斜率得到更好的数据拟合曲线。

尽可能地使成本函数最小化,我们试得θ1和θ0的结果趋于分别在0.12和250左右。 在我们的图表上绘制这些值似乎将我们的值放在了最内圈的中心。

接下来的问题就是如何获得最好的成本函数?
以上内容翻译整理自https://www.coursera.org/learn/machine-learning,课程免费并且讲的很好,这里仅做学习分享。

