文中所有论文链接均可点击直接下载
复杂网络在复杂性研究中占据着什么样的地位?
复杂网络是对复杂系统的一种抽象。研究复杂系统有很多角度和方法,而复杂网络正是其中的一种。
复杂系统由大量相互关联,相互作用的个体组成。而复杂网络关注系统中的个体相互作用而成的网络的结构,通过构建复杂网络,可以帮助我们从系统相互作用网络的拓扑结构的角度来理解复杂系统。换言之,网络拓扑结构的信息是研究系统性质和功能的基础,也是理解系统功能的关键。
复杂网络无处不在
复杂网络无处不在,几乎覆盖了我们能想到的所有领域,现代生活的基础是电力网,获取信息的渠道是互联网,每个人都身处于社会网络之中,你的出行依赖于交通网络,每个人脑都是一个巨大的神经网络,你的体内无时无刻不在发生着蛋白质的相互作用,而这些相互作用可以被建模为蛋白质相互作用网络,等等等等。
复杂网络研究关心的问题
总体而言,复杂网络研究关心的问题可以分为如下四个子类,各个子类之间并非完全独立,而是具有相互继承的关系。
- 首先,复杂网络研究关注如何建立一个复杂网络。
- 其次,我们关注如何定量刻画复杂网络,如何描述复杂网络的结构及其性质,我们开发了多种方法,例如统计网络的度分布情况,集聚系数等。
- 进而,我们关注网络是如何发展成这种结构的,也就是网络的演化过程如何描述。
- 最后,我们可以思考网络这种特定的结构的后果是什么。例如,网络的这种结构是否具有鲁棒性?网络上的动力学行为如何刻画等等。
值得注意的是,最后一个问题通常被我们称为正问题,即在已知结构的情况下去分析网络的性质。而第一个问题则是复杂网络中的反问题:在许多情况下,我们并不知道网络结构,因此我们首先要通过某种方式(例如网络重构方法)去建立网络结构。
复杂网络分析初步:一些基本的统计量
在复杂网络分析的过程中,有一些基本的统计量非常重要,他们可以粗略的刻画网络的结构特性,是复杂网络分析过程中的基础指标。我们在这里粗略概括如下:
- 度
度是针对一个节点的统计量,即一个节点的邻居数量。进一步的,在有向图中,度又分为入度和出度,入度指的是指向自己的邻居数量,出度指的是自己指向的邻居数量。 - 平均度
平均度,指的是一个网络中所有节点的度的平均数,他可以粗略地衡量网络的集聚程度:平均度高的网络集聚程度高。 - 度分布
度分布可以衡量在网络中随机选取一个节点,他的度值恰好是k的概率是多少。通常我们会将度分布化成一条曲线。他的横坐标是度值k,纵坐标是随机选取一个节点,节点的度值恰好为k的概率,也就是度值为k的节点数 / 总节点数:Nk / N。 - 路径
复杂网络中的路径即是其字面意思,从一个节点走到另一个节点的通路。值得注意的是,一般定义下的路径可以有环,可以往回走。所以我们在分析中,更常用的是两点之间的“最短路径”。 - 距离与网络直径
两个节点之间的距离即是两点之间的最短路径长度。如果这两个节点并不联通,那么他们之间的距离是正无穷。另外,在有向图中,连边具有方向,就如同一个箭头。在这种情况下,只存在从箭尾指向箭头的路径,反过来则不行,所以在有向图中,从A到B的距离和从B到A的距离往往不一样。一个网络中的最大距离被称为网络的“直径”。 - 介数
介数是一个针对节点的统计量,节点A的介数指的是通过节点A的最短路径条数。如果一个大介数节点被删除,将会对网络整体的连通性产生重要的影响。 - 集聚系数
集聚系数是衡量网络是否“紧密聚集”,即网络内部是否有很多成团现象的指标。一个节点的集聚系数是这个节点的所有邻居中,实际相连的节点对占全部可能相连的节点对的比例。而一个网络的平均集聚系数则是网络内每个节点的集聚系数的平均值,因此可以看出,集聚系数是一个0到1之间的值,越偏向0说明网络越松散,否则越集聚。 - 邻接矩阵
邻接矩阵是一个矩阵,他存在的意义是具体的描述一个网络的拓扑结构,包括每对节点的连接方式:邻接矩阵A是一个方阵,他的边长等于节点数量。如果Aij = 1,说明节点i和j之间存在连边,否则不存在。
随机图:ER Model
随机图是最基本的一个网络模型,因为他的许多性质是随机的,所以在科研中的作用是经常作为baseline,与其他图结构进行性质上的比较,因此我们有必要了解随机图的结构性质。随机图有很多特点,例如,在度分布方面,随机图在节点数量很多,平均度很小的时候,其度分布符合泊松分布。
随机网络有两种机制模型,他们描述了两种不同但性质相似的随机网络的建立过程。第一种随机网络模型被定义为C(N,p) Model,他的意思是有N个节点,任何两个节点都以概率p相连接的网络。第二种随机网络被定义为C(N,L) Model,他的意思是有N个节点,和L条随机放置在图上的连边的网络,在这种模型中,L条连边以均等的概率连接在任意两个节点之间
我们知道,在现实的社交网络中,有的人知名度很高,他们的度很大,而也有很多人的社交圈子很窄,他们的度很小。这种的度极大和极小的节点被称为奇异点。值得一提的是,随机图内没有奇异点,因为随机图内每个节点被连接的概率都是均等的,所以在随机图中,产生奇异点是一个几乎可以忽略的小概率事件。
另外,我们还应知道,在C(N,p)模型中,随机网络的平均距离随节点数量的变化关系为对数关系,具体而言,d= logN / logk.其中d为平均距离,k为节点的平均度。随机网络结构造成的另一后果是:随机网络的集聚系数很低,相比于随机网络而言,实际的网络更为集聚。
小世界网络
我们经常听到一个名为“六度分隔”的理论,他的意思是说,在大多数情况下,这个世界上的任何两个人之间,只需要5、6个人就能相互认识。六度分隔理论并非无稽之谈,而是一个科学实验的结果:1967年,哈佛大学的社会心理学家米尔格兰姆(Stanley Milgram)设 计了一个连锁信件实验。他将一套连锁信件随机发送给居住在内布拉斯加州奥马哈的160个人,信中放了一个波士顿股票经纪人的名字,信中要求每个收信人将这套信寄给自己认为是比较接近那个股票经纪人的朋友。朋友收信后照此办理。最终,大部分信件在经过五、六个步骤后都抵达了该股票经纪人。我们会认识到这个世界具有“小世界特性”,而小世界网络不但能刻画这种特性,而且他作为一种数学模型,可以帮助我们更深刻的理解我们的世界,我们的大脑和其他许许多多具有小世界特性的现实复杂网络。
1998年,邓肯·瓦特和斯托加茨在《自然》杂志上发表了关于小世界网络模型的论文《Collectivedynamics of‘small-world’ networks》,首次提出并从数学上定义了小世界概念,并预言它会在社会、自然、科学技术等领域具有重要的研究价值。所谓小世界网络,就是相对于同等规模节点的随机网络,具有较短的平均路径长度和较大的聚类系数特征的网络模型。以前,人们认为网络分为完全规则网和完全随机网,这两类网络具有各自的特征。规则网具有较大的特征路径长度,聚类系数也较大,而随机网络具有较小的特征路径长度,但是聚类系数较小。难道特征路径长度较大(小)一定伴随着较大(小)的聚类系数?另外,很多现实中的网络如电网,交通网络,脑神经网络,社交网络,食物链等都表现出小世界特性,即具有较小的特征路径长度。
Watt采用一种随机重连边的方法,以探求位于规则网和随机网的中间地带。如图:

规则网有N个节点,每个节点与K个最近邻节点相连(K是偶数)。上图的规则网有20个节点,每个节点与相邻的4个节点互联。然后,对每条边进行以概率P进行随机重连(0<=P<=1)。P=0时对应规则网,P=1时对应完全随机网,通过调整P的值可以得到位于两种网络中间的网络模型,然后探究其特征。
通过实验并统计网络呈现出的特征,得到下图(归一化处理后)

可见,在P较小时(P<0.01),特征路径长度急剧下降,而聚类系数几乎没有变化。这样,我们发现这些网络具有较短的特征路径长度和较大的聚类系数,我们称其为“小世界网络”。为了验证试验结果的稳定性,作者采用了多种不同的规则网络和随机重连算法进行试验,得到了相同的结果.
那么为什么会出现这种特征呢?关键是“捷径”的添加。所谓“捷径”,即随机重连过程中添加的长边。如试验中P<0.01时,规则网络中会添加极少量的长边,不仅使长边两端的节点(假定A和B)路径长度变小,而且A节点的和B节点的邻居乃至B的邻居的邻居之间距离都变小了。于此同时,随机重连对网络的聚类系数影响很小,至多是线性减少。于是,P较小时生成的网络具有小世界特征。当P较大时,随着长边的增多,网络的聚类系数开始迅速变小,向完全随机化网络演变。
在论文中,通过对三个现实中的案例:美国西部的电力网络、电影演员的协作网络、蠕虫的神经网络分析,发现三者都具有小世界特征,如下图。

人们发现在具有小世界特征的动力系统中,信息的传播能力、计算能力等都得到了增强。瓦茨认为;局部行为导致了全局性的结果,而局部动态特性和全局动态特性之间的关系,则主要依赖于网络的结构。在这篇论文中,作者利用人群中传染病的传播、博弈论中合作的演化、元胞自动机的计算能力、耦合相位振子的同步等具有小世界特征的动力系统进行了研究,并对小世界的前途进行了展望。
无标度网络
无标度网络和小世界网络一样,都是复杂网络分析中不得不了解的一环。已经证实现实中包括社交网络、科学家合作网络、蛋白质调控网络,新陈代谢网络,万维网在内的不同系统中的大量网络结构都符合无标度性质。无标度网络的重要性不言而喻。
无标度网络是指那些度分布符合幂律分布的网络,他有两大基本特征:
1.无标度网络具有自相似结构,
2.两极分化,高度弥散。
我们会接下来会对无标度网络的定义进行简单的理解:
我们已经在前面讨论过度分布的概念,而在无标度网络中,网络的度分布复合幂律分布,这是指随机选取一个节点,他的度为k的概率正比于k的-γ次方。
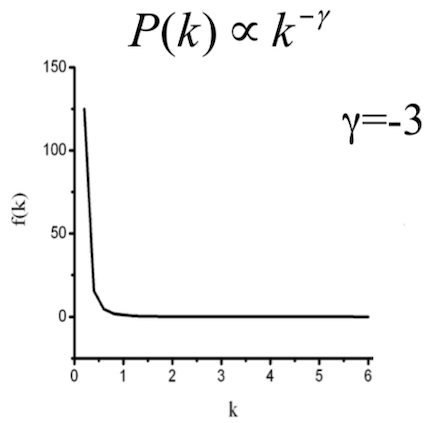
对于这种曲线,我们很难直观的看出其分布是否是幂律分布,一个常用的处理方法是在等式的两端取对数,如果原分布是幂律分布的话,那么分布曲线在双对数坐标下就会变成一条直线:即lnP(k)∝−γ*lnk。
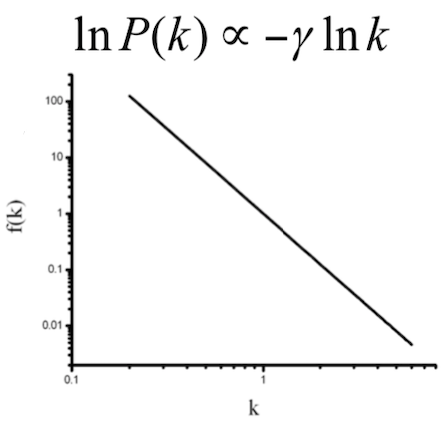
幂律分布可以帮助我们理解两极分化,高度弥散的特征,首先,在幂律分布的网络中,不同节点的度数往往会横跨多个数量级:有度很大的节点,也有度很小的节点,网络的度数呈现“两极分化”的特点,另外,当k很小时,P(k)很大,这意味着大量的节点的度都非常小,只有少部分的节点是大度节点,网络呈现”高度弥散“的特点。
无标度网络的自相似性指的是网络的局部和整体在结构特性上是相似的,也就是说网络不具有明显的尺度特征,这也是“无标度”这个名字的由来。
无标度网络是如何演化出来的?一个最被广泛接受的模型BA模型《Emergence of scaling in random networks》。在BA模型中,节点数目是不断增加的,网络的规模在不断的增大。另外,网络 中不断产生的新的节点更倾向于和那些连接度较大的节点相连,即遵循偏好连接的机制。在BA模型中,增长和偏好链接缺一不可。
无标度网络和小世界网络的区别
无标度网络和小世界网络的最大区别是他们的度分布的差别
- 无标度网络的度分布式幂函数
- 小世界是钟形正态分布,与random network 的度分布相似,点和点之间的连接时随机的
- 小世界点和点之间的路径最短
- 无标度网络有巨集团和剩余度的涌现,也就是说巨集团基本代表网络的连接密度,少数的点有大量的连线(这样的点称之为Hub点),大多数点有少量或者没有连线。数Hub点对无标度网络的运行起着主导的作用。
网络中的度相关(匹配性)
网络的平均度是一种对网络的粗略描述,度分布让我们对网络的认识更具体一些,但即便度分布已经很具体,它也不能完全地刻画网络的结构特性,在某些情况下,具有相同度分布的网络可能展现出不同的性质或行为。为此,我们需要进一步深入,了解另一指标:匹配性(又称度相关)。
基本上,我们的思路是这样的:度分布描述了随机在网络上选取一个节点,它的度为k的概率。而度相关则描述了在网络中随机选取一条边两端的节点,他们的度分别为j和k的联合概率,因此我们可以将度相关理解为2阶的度分布。
如果网络中的随机选择的一条边两端节点的度值是完全随机的,也就是说网络中的两个节点之间是否有连边与这两个节点的度值无关,则称这个网络不具有度相关性,否则,我们就认为这个网络有度相关性。
进一步的,如果总体上来说,大度节点更倾向于连接大度节点,我们称这个网络是正相关(同配)的,否则,称这个网络为负相关(异配)的。为了刻画这种相关的程度,我们还可以发明“同配系数”作为量化指标。
研究网络上的度相除了赋予我们更深刻的理解网络结构的能力之外,还具有很重要的现实意义。例如,社会网络、科学家合作网络,演员合作网络都是典型的同配网络,影响力大的人更倾向于认识影响力大的人,而蛋白质交互网络与技术网络则更多是异配的。以上的网络通常都符合幂律分布,但因为匹配性的差异而具有不同的性质。研究这些性质的成因与影响,是复杂网络分析中的重要课题。
加权网络
网络连边上的权重衡量的是节点之间相互作用的强度。我们研究加权网络,是为了通过引入权重来从新的视角更好地理解和衡量网络的性质。因此加权网络关心的问题就可以被大致归纳为如下两类:
1.我们如何对网络加权
2.如何加权更好地理解网络的性质。
如何给连边加权?
为了能够更好的刻画节点之间相互作用的强度,我们在不同的现实问题中需要仔细考虑权重的设置标准。在已有物理量的情况下,例如,在航空网络中,我们可以选取两地之间的航班数量,座位数量或里程作为权重,在因特网中可以选取带宽作为权重等等。而在没有物理量的网络中,我们可以定义抽象权重,例如科学家合作网络的合著文章数等。
权重如何帮助我们更好地理解网络的性质?
一方面,权重的加入为我们提供了审视网络的全新视角,例如,我们可以衡量网络的权重分布(而非度分布),也可以考察节点的点强度(即strength,结点所有连边上的权重的总和)。另一方面,权重的加入也可以让我们更精确的衡量原有统计指标的意义:例如加权网络上的权重如果代表了距离的话,那么网络上的路径长度的计算方式就需要随之进行改变,进而,最短路径、介数、平均最短距离、网络直径等指标都可以得到新的计算。加权网络的集聚系数也与无权网的上的计算方法有所不同。
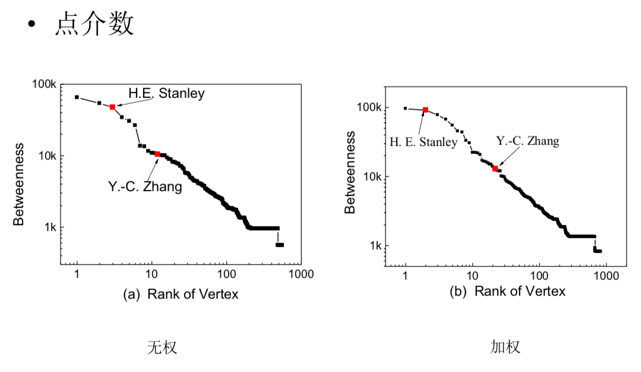
上图为无权和加权的科学家合作网上节点的介数排序,虽然大致趋势相同,但加权网更好的衡量了科学家对社区的贡献。
若要深入的研究权重在网络结构中的地位和作用,一个可靠的技术路线是通过不同的技术手段对权重进行调整,并分别观察权重的改变将对那些网络性质指标产生何种影响。这需要我们确定权重调整的方式,选取好相应的网络并且寻找刻画权重影响的结构。这里为大家推荐几篇相关的文献,他们大体采取了类似的思路,并且取得了不错的研究成果。
复杂网络中的社团结构
研究一个复杂网络,我们可以从多个角度入手,从微观角度,我们可以聚焦在节点上,关注他的度、介数、中心性等性质,从宏观角度,我们可以关注整个网络的聚集程度,度分布等性质。而社团结构则介于微观和宏观之间,是我们研究复杂网络的一种中观视角。
如果从描述性的角度来定义社团结构,它指的是复杂网络中的一个局部,这个局部内部的链接很稠密,但这个局部与其他社团的链接则很稀疏。找到复杂网络中的社团可以帮助我们更好的从中观尺度认识网络。而如何找到社团结构就成了复杂网络中的社团这一研究领域的一个经典问题,本小节的大部分介绍也将围绕着这一问题展开。
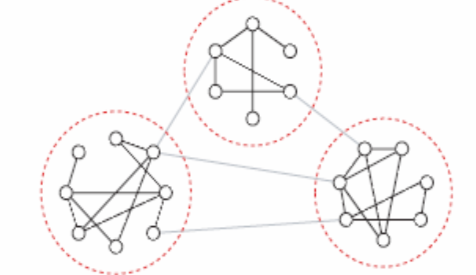
如何寻找网络中的社团结构这一问题可以被进一步的区分为两个小的子问题:首先,我们如何将网络尽量合理的切割成多个社团,使得各个社团内部链接比较稠密,而社团之间链接却比较稀疏?其次,我们如何通过某种可靠的方法量化某种划分的“好坏”?
要解决上述的第二种问题,人们发明了很多种对社团划分结果的评价方法,其中最广为认可的一种方法之一叫做基于Q函数的数学评价方法。Q函数的输入是对网络进行社团划分的结果,包括每个节点所属的社团信息,而Q函数的输出则是一个标量,表示对该划分结果的评价,一般来说,Q函数的输出值介于0到1之间,越接近1表示该划分结果越好。
要解决第一种问题,我们需要发明一种寻找社团结构的方法。事实上,科学家们经过多年的探索,已经发明了很多这种方法,这些方法可以大致的分为三个主要类别,我们将三个类别及其主要的代表方法列举如下:
1.基于网络拓扑结构的方法,层次聚类法是这种方法的主要代表。这种方法的特征是只用网络的拓扑结构信息,即可在不同层次将网络分为几个社团,最低的层次是指每一个节点都是一个单独的社团,而最高层次是指整个网络是一个大社团,一般来说,我们认为最优划分就在其中的某个层次。Community structure in social and biological networks [2001]Michelle Girvan,M. E. J. Newman
2.基于网络上的动力学的方法,这种方法的核心思路是在网络上定义某种动力学,让网络进行演化,对时间演化数据序列进行分析,从而得到社团结构。
Detecting fuzzy community structures in complex networks with a Potts model [2004]Joerg Reichardt,Stefan Bornholdt
3.基于Q函数优化的方法,这种方法的本质是将社团划分问题转化为一个优化问题,在前文中我们已经提过Q函数是一种对社团划分结果进行评价的数学方法,既然有了对结果的评价,我们就可以以Q函数的评价结果最大为目标,引入诸如贪婪算法、模拟退火或极值优化等方法对该目标进行优化。
Fast algorithm for detecting community structure in networks [2003]M. E. J. Newman
网络上的节点重要性
在现实网络中,有些节点对网络整体非常重要,有些节点则无关紧要。将某种生物从当地食物网中擦除(即全部消灭)很有可能对当地的整个生态系统造成毁灭性的打击。社交网络中的某些种子用户发出的信息很可能影响到全网的舆情走向,而同样的信息被不重要的人发送则并不会影响整个网络的状态。因此,我们需要用一种度量指标,即测度,来合理的度量节点的重要性(也称为中心性)。
有很多种测度可以用来衡量节点的中心性,其中最简单的一种便是节点的度,我们将其称为“度中心性”:度越大的节点中心性越高,这背后的潜在假设是,如果一个人认识的人越多,那么它的影响力则越大,这个假设基本上是合理的,但度中心性只能粗略的衡量网络中的节点影响力。为了克服度中心性的缺点,更详细的从不同角度刻画节点的中心性,人们相继提出了特征向量中心性,介数中心性,接近度中心性等等。
另外,值得一提的是,让早期的Google搜索引擎一骑绝尘的PageRank算法,也是节点中心性测度的一种应用。在同期的搜索引擎大多采用机器+人工的方式对搜索结果进行排序的情况下,Google率先采用了一种新的思路:将整个web看成一个图,网页就是其中的一个节点,而网页之间的超链接可以作为有向边。进而使用节点中心性排序算法对搜索结果进行排序。
有关PageRank算法的详细过程参考:深入浅出PageRank算法
网络上的动力学
网络上的动力学,即一种对网络上的节点之间如何相互影响的描述,例如,在传染病动力学中,所有的节点都有健康,染病,恢复这三种状态,如果在某时刻,一个节点的大部分邻居都处于染病状态,那么下一时刻这一节点很可能遭受感染——其自身的状态将会由健康变为染病。网络上的动力学多种多样,有的可以用概率模型描述(例如这里提到的传染模型),有的则需要用微分方程描述(弹簧振子模型等),还有规则表等等(布尔网络模型等)。
我们前述的所有讨论都基于对网络拓扑结构的分析,要知道,对网络结构的研究只是迈出了复杂网络研究的第一步,而对网络上的动力学的理解则可以让我们迈出下一步:认识网络结构和功能的关系,理解和解释网络的行为。
[1]复杂网络分析入门路径
[2]浅谈小世界网络
[3]无标度网络和小世界网络的区别

