跳到主要内容

【深度学习】反卷积输出尺寸计算公式

neunms    2020年8月5日 16:29:04

反卷积英文翻译为：Deconvolution或Transposed Convolution或Fractional-strided  Convolutions。
在机器学习中，反卷积是从低分辨率映射到大分辨率的过程，用于扩大图像尺寸。
反卷积是一种特殊的正向卷积，而不是卷积的反过程。
 
本文将从直观的角度，推导反卷积运算输出尺寸的计算公式。

符号约定：  
输入尺寸（input）: [公式]
卷积核大小（kernel size）: [公式]
步幅（stride）: [公式]
边界扩充（padding）: [公式]
输出尺寸（output）: [公式]

卷积输出尺寸计算
卷积过程示例如图1所示，蓝色方块为输入，绿色方块为输出，灰色方块为卷积核。经过卷积计算，输出尺寸计算公式：
[公式]
公式(1)
图1：卷积过程示例
例1：卷积运算输出尺寸计算 
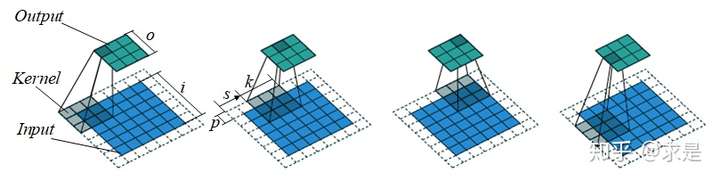
以图1中的卷积过程为例，输入尺寸，卷积核大小，步幅，扩充分别为：[公式]，代入公式（1）：
[公式]
即输出尺寸为3。

反卷积输出尺寸计算
第一步：对输入进行stride变换，如图2所示。
 反卷积中，stride可理解为为在输入的相邻元素之间添加 [公式]个零元素。变换后的尺寸为：
[公式]
公式(2)
图2：反卷积Stride过程
例：图2的stride过程中，输入和步长分别为[公式]，则[公式]
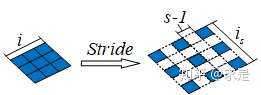
第二步：对stride变换后的图片按照卷积形式求解输出尺寸。
即，将式（2）带入式（1）：
[公式]
公式(3)
注意：由于在第一步中已经将stride进行运算，式（3）中的s此时恒等于1，即[公式]。
第三步：求解反卷积输出尺寸。
 将式（2）带入式（3），化简得：
[公式]
公式(4)

式（4）恒为整数，可将[·]运算符去掉，即得到反卷积输出的尺寸计算公式：
[公式]
公式(5)
比较式（5）与式（1）可知，当步长 [公式] 时，卷积与反卷积输出尺寸计算公式相同。这种情况下反卷积即为卷积，也说明了反卷积是一种特殊的卷积，而非卷积的逆过程。
下面给出反卷积运算输出尺寸的计算示例。

例2：反卷积输出尺寸计算(s=1) 
图3：反卷积过程示例（s=1）
如图3所示，反卷积过程各参数分别为： [公式]，代入式（5）可得：[公式] 即输出尺寸为4。

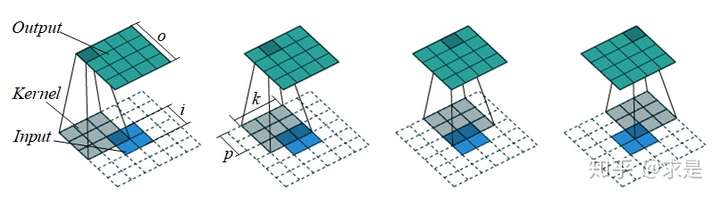
例3：反卷积输出尺寸计算(s>1) 
图4：反卷积输出尺寸计算示例(s>1)
如图4所示，反卷积过程各参数分别为： [公式] ，代入式（5）可得： [公式]
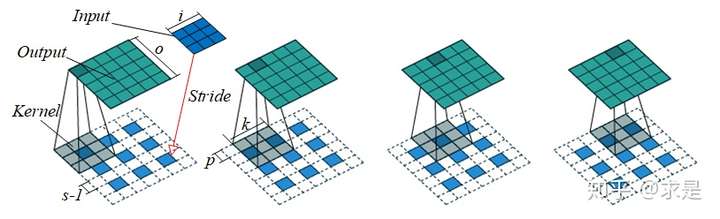
即输出尺寸为5。

转载自：https://zhuanlan.zhihu.com/p/57348649
最近更新： 2020年8月5日 21:01:33
浏览： 6.0K

[[total]] 条评论

添加评论
  1. [[item.time]]
    [[item.user.username]] [[item.floor]]楼
  2. 点击加载更多……
  3. 添加评论

添加评论 登录后即可回复